18. Advanced methods

This page documents advanced features of ESPResSo. Be sure to read the relevant literature before using them.

18.1. Creating bonds when particles collide

Please cite [Arnold et al., 2013] when using dynamic binding.

With the help of this feature, bonds between particles can be created automatically during the simulation, every time two particles collide. This is useful for simulations of chemical reactions and irreversible adhesion processes. Both, sliding and non-sliding contacts can be created.

The collision detection is controlled via the system.collision_detection attribute, which is an instance of the class CollisionDetection.

Several protocols are available for different types of dynamic binding. The currently active collision mode can be removed by assigning None or Off to the system.collision_detection.protocol attribute.

18.1.1. Bind centers

Add a pair-bond between two particles at their first collision. By making the bonded interaction stiff enough, the particles can be held together after the collision. Note that the particles can still slide on each others’ surface, as the pair bond is not directional. This protocol affects all particle types. This protocol is set up with BindCenters as follows:

import espressomd
import espressomd.interactions
import espressomd.collision_detection
system = espressomd.System(box_l=[1, 1, 1])
bond_centers = espressomd.interactions.HarmonicBond(k=1000, r_0=0.1)
system.bonded_inter.add(bond_centers)
system.collision_detection.protocol = espressomd.collision_detection.BindCenters(
    distance=0.1, bond_centers=bond_centers)

The parameters are as follows:

• distance is the distance between two particles at which the binding is triggered. This cutoff distance, 0.1 in the example above, is typically chosen slightly larger than the particle diameter. It is also a good choice for the equilibrium length of the bond.

• bond_centers is the bonded interaction to be created between the particles (an instance of HarmonicBond in the example above). No guarantees are made regarding which of the two colliding particles gets the bond. Once there is a bond of this type on any of the colliding particles, no further binding occurs for this pair of particles.

Note

The following features are required: COLLISION_DETECTION.

18.1.2. Bind at point of collision

Add two pair-bonds between two particles and two automatically generated virtual sites at their first collision.

This protocol prevents sliding of the colliding particles at the contact point. This is achieved by creating two virtual sites at the point of collision. They are rigidly connected to each of the colliding particles. Then, either a pair bond is added between the virtual sites, or an angular bond is added between the two colliding particles and the virtual particles. In the latter case, the virtual particles are the centers of the angle potentials (particle 2 in the description of the angle potential, see Bond-angle interactions). Due to the rigid connection between each of the colliding particles and their respective virtual sites, sliding at the contact point is no longer possible. See Rigid arrangements of particles for details. This protocol affects all particle types.

In addition to the bond between the virtual sites, a bond between the colliding particles is also created. You can either use a real bonded interaction to prevent wobbling around the point of contact or you can use espressomd.interactions.Virtual which acts as a marker, only.

This protocol is set up with BindAtPointOfCollision as follows:

import espressomd
import espressomd.interactions
import espressomd.collision_detection
system = espressomd.System(box_l=[1, 1, 1])
bond_centers = espressomd.interactions.HarmonicBond(k=1000, r_0=0.1)
bond_vs = espressomd.interactions.HarmonicBond(k=10000, r_0=0.02)
system.bonded_inter.add(bond_centers)
system.bonded_inter.add(bond_vs)
system.collision_detection.protocol = espressomd.collision_detection.BindAtPointOfCollision(
    distance=0.1,
    bond_centers=bond_centers,
    bond_vs=bond_vs,
    part_type_vs=1,
    vs_placement=0.5)

The parameters distance and bond_centers have the same meaning as in the Bind centers protocol. The remaining parameters are as follows:

• bond_vs is the bond to be added between the two virtual sites created on collision. This is either a pair-bond with an equilibrium length matching the distance between the virtual sites, or an angle bond fully stretched in its equilibrium configuration.

• part_type_vs is the particle type assigned to the virtual sites created on collision. In nearly all cases, no non-bonded interactions should be defined for this particle type.

• vs_placement controls where the virtual sites are placed on the line connecting the colliding particles. A value of 0 means that the virtual sites are placed at the same position as the colliding particles on which they are based. A value of 0.5 will result in the virtual sites being placed at the mid-point between the two colliding particles. A value of 1 will result the virtual site associated to the first colliding particle to be placed at the position of the second colliding particle. In most cases, 0.5, is a good choice. Then, the bond connecting the virtual sites should have an equilibrium length of zero.

Note

The following features are required: COLLISION_DETECTION, VIRTUAL_SITES_RELATIVE.

18.1.3. Glue to surface

Attach small particles to the surface of a large particle. The bond can be made irreversible.

Several small particles can be bound to a large particle but not vice versa. The small particles can change type after collision to become inert.

This protocol is set up with GlueToSurface as follows:

import espressomd
import espressomd.interactions
import espressomd.collision_detection
system = espressomd.System(box_l=[1, 1, 1])
bond_centers = espressomd.interactions.HarmonicBond(k=1000, r_0=0.1)
bond_vs = espressomd.interactions.HarmonicBond(k=10000, r_0=0.02)
system.bonded_inter.add(bond_centers)
system.bonded_inter.add(bond_vs)
system.collision_detection.protocol = espressomd.collision_detection.GlueToSurface(
    distance=0.1,
    distance_glued_particle_to_vs=0.02,
    bond_centers=bond_centers,
    bond_vs=bond_vs,
    part_type_vs=1,
    part_type_to_attach_vs_to=2,
    part_type_to_be_glued=3,
    part_type_after_glueing=4)

On collision, a single virtual site is placed and related to the large particle. Then a bond (bond_centers) connects the large and the small particle. A second bond (bond_vs) connects the virtual site and the small particle. Further required parameters are:

• part_type_to_attach_vs_to: Type of the particle to which the virtual site is attached, i.e., the large particle.

• part_type_to_be_glued: Type of the particle bound to the virtual site (the small particle).

• part_type_after_glueing: The type assigned to the particle bound to the virtual site (small particle) after the collision.

• part_type_vs: Particle type assigned to the virtual site created during the collision.

• distance_glued_particle_to_vs: Distance of the virtual site to the particle being bound to it (small particle), as a fraction of the pair distance.

Note: When the type of a particle is changed on collision, this makes the particle inert with regards to further collisions. Should a particle of type part_type_to_be_glued collide with two particles in a single time step, no guarantees are made with regards to which partner is selected. In particular, there is no guarantee that the choice is unbiased.

Note

The following features are required: COLLISION_DETECTION, VIRTUAL_SITES_RELATIVE.

18.2. Deleting bonds when particles are pulled apart

With this feature, bonds between particles can be deleted automatically when the bond length exceeds a critical distance. This is used to model breakable bonds.

The bond breakage action is specified for individual bonds via the system bond_breakage attribute.

Several modes are available:

• "delete_bond": delete a bond from the first particle

• "revert_bind_at_point_of_collision": delete a bond between the virtual site

• "none": cancel an existing bond breakage specification

For a pair bond, the breakage distance refers to the minimum image distance between the primary particle and its bond partner. For an angle bond, the distance refers to the distance between the two bond partners of the primary particle. Example:

import espressomd
import espressomd.interactions
import espressomd.bond_breakage
import numpy as np

system = espressomd.System(box_l=[10] * 3)
system.cell_system.skin = 0.4
system.time_step = 0.1
system.min_global_cut = 2.

h1 = espressomd.interactions.HarmonicBond(k=0.01, r_0=0.4)
h2 = espressomd.interactions.HarmonicBond(k=0.01, r_0=0.5)
system.bonded_inter.add(h1)
system.bonded_inter.add(h2)
system.bond_breakage[h1] = espressomd.bond_breakage.BreakageSpec(
    breakage_length=0.5, action_type="delete_bond")

p1 = system.part.add(id=1, pos=[0.00, 0.0, 0.0], v=[0.0, 0.0, 0.0])
p2 = system.part.add(id=2, pos=[0.46, 0.0, 0.0], v=[0.1, 0.0, 0.0])
p1.add_bond((h1, p2))
p1.add_bond((h2, p2))
for i in range(3):
    system.integrator.run(2)
    bond_length = np.linalg.norm(system.distance_vec(p1, p2))
    print(f"length = {bond_length:.2f}, bonds = {p1.bonds}")

Output:

length = 0.48, bonds = ((<HarmonicBond({'r_0': 0.4, 'k': 0.01})>, 2), (<HarmonicBond({'r_0': 0.5, 'k': 0.01})>, 2))
length = 0.50, bonds = ((<HarmonicBond({'r_0': 0.4, 'k': 0.01})>, 2), (<HarmonicBond({'r_0': 0.5, 'k': 0.01})>, 2))
length = 0.52, bonds = ((<HarmonicBond({'r_0': 0.5, 'k': 0.01})>, 2),)

Please note there is no special treatment for the energy released or consumed by bond removal. This can lead to physical inconsistencies.

18.3. Modeling reversible bonds

The collision detection and bond breakage features can be combined to model reversible bonds.

Two combinations are possible:

• "delete_bond" mode for breakable bonds together with the Bind centers protocol of collision detection: used to create or delete a bond between two real particles

• "revert_bind_at_point_of_collision" mode for breakable bonds together with the Bind at point of collision protocol of collision detection: used to create or delete virtual sites (the implicitly created bond between the real particles isn’t affected)

Please note that virtual sites are not automatically removed from the simulation, therefore the particle number will increase. If you want to remove virtual sites, you need to do so manually, either by tracking which virtual sites were introduced by collision detection, or by periodically looping over the particle list and removing virtual sites which have no corresponding bond.

18.4. Immersed Boundary Method for soft elastic objects

Please contact the Biofluid Simulation and Modeling Group at the University of Bayreuth if you plan to use this feature.

With the Immersed Boundary Method (IBM), soft particles are considered as an infinitely thin shell filled with liquid (see e.g. [Crowl and Fogelson, 2010, Krüger, 2012, Peskin, 2002]). When the shell is deformed by an external flow, it responds with elastic restoring forces which are transmitted into the fluid. In the present case, the inner and outer liquid are of the same type and are simulated using lattice-Boltzmann.

Numerically, the shell is discretized by a set of marker points connected by triangles. The marker points are advected with exactly the local fluid velocity, i.e., they do not possess a mass nor a friction coefficient (this is different from the Object-in-fluid method below). We implement these marker points as virtual tracer particles which are not integrated using the usual velocity-Verlet scheme, but instead are propagated using a simple Euler algorithm with the local fluid velocity.

The immersed boundary method consists of two components, which can be used independently:

• Inertialess lattice-Boltzmann tracers implemented as virtual sites

• Interactions providing the elastic forces for the particles forming the surface. These are described in Immersed Boundary Method interactions.

For a more detailed description, see e.g. [Guckenberger and Gekle, 2017] or contact us. This feature probably does not work with advanced LB features such as electrokinetics.

A sample script is provided in the /samples/immersed_boundary/ directory.

18.5. Object-in-fluid

If you plan to use this feature, please contact the Cell-in-fluid Research Group at the University of Zilina: ivan.cimrak@fri.uniza.sk or iveta.jancigova@fri.uniza.sk.

When using this module, please cite [Cimrák et al., 2014] (BibTeX key cimrak14a in doc/bibliography.bib) and [Cimrák et al., 2012] (BibTeX key cimrak12a in doc/bibliography.bib)

This documentation introduces the features of module Object-in-fluid (OIF). Even though ESPResSo was not primarily intended to work with closed objects, it is a flexible package and appears very suitable when one wants to model closed objects with elastic properties, especially if they are immersed in a moving fluid. Here we describe the module itself and offer some additional information to get you started with. Additionally, we provide a step by step tutorial that will show you how to use this module.

The OIF module was developed for simulations of red blood cells flowing through microfluidic devices and therefore the elasticity features were designed with this application in mind. However, they are completely tunable and can be modified easily to allow the user to model any elastic object moving in fluid flow.

18.5.1. Triangulations of elastic objects

To create an elastic object, we need a triangulation of the surface of this object. Sample triangulations are provided at http://cell-in-fluid.fri.uniza.sk/en/content/oif-espresso. Users can create their own meshes, for example in gmsh, salome or any other meshing software. Two files are needed, one for the node positions and one for the connectivity of triangles:

• oif_nodes.dat should contain triplets of floats (one triplet per line), where each triplet represents the \(x, y\) and \(z\) coordinates of one node of the surface triangulation. No additional information should be written in this file, so this means that the number of lines is equals to the number of surface nodes. The coordinates of the nodes should be specified in such a way that the approximate center of mass of the object corresponds to the origin (0,0,0). This is for convenience when placing the objects at desired locations later.

• oif_triangles.dat should contain triplets of numbers, this time integers. These integers refer to the IDs of the nodes in the oif_nodes.dat file and specify which three nodes form a triangle. Please note that the nodes’ IDs start at 0, i.e. the node written in the first line of oif_nodes.dat has ID 0, the node in the second line, has ID 1, etc.

18.5.2. Description of sample script

Note

The following features are required: EXTERNAL_FORCES, MASS, SOFT_SPHERE

The script described in this section is available in samples/object-in-fluid/motivation.py and also at http://cell-in-fluid.fri.uniza.sk/en/content/oif-espresso.

In the first few lines, the script includes several imports related to the red blood cell model, fluid, boundaries and interactions. Then we have:

system = espressomd.System(box_l=(22, 14, 15))
system.time_step = 0.1
system.cell_system.skin = 0.2

Here we set up a system and its most important parameters. The skin depth tunes the system’s performance. The one important thing a user needs to know about it is that it has to be strictly less than half the grid size.

box_l sets up the dimensions of the 3D simulation box. You might wonder what the units are. For now, you can think of them as micrometers, we will return to them later.

time_step is the time step that will be used in the simulation, for the purposes here, in microseconds. It allows separate specification of time step for the particles and for the fluid. This is useful when one takes into account also thermal fluctuations relevant on molecular level, however, for us, both of these time steps will mostly be identical.

18.5.2.1. Specification of immersed objects

cell_type = OifCellType(nodesfile="input/rbc374nodes.dat",
    trianglesfile="input/rbc374triangles.dat", system=system,
    ks=0.02, kb=0.016, kal=0.02, kag=0.9, kv=0.5, resize=[2.0, 2.0, 2.0])

We do not create elastic objects directly but rather each one has to correspond to a template, cell_type, that has been created first. The advantage of this approach is clear when creating many objects of the same type that only differ by e.g. position or rotation, because in such case it significantly speeds up the creation of objects that are just copies of the same template.

The three mandatory arguments are nodes-file and triangles-file that specify input data files with desired triangulation and system that specifies the ESPResSo system. The relaxed mesh triangles should be as close to equilateral as possible with average edge length approximately equal to the space discretisation step \(\Delta x\). While these lengths vary during the simulation, the connectivity of the mesh nodes never changes. Basic meshes can be downloaded from our website. This script assumes that the two necessary files are located inside an input directory that resides in the same folder as the simulation script.

All other arguments are optional. resize defines resizing in the \(x, y, z\) directions with respect to unit size of the object, so in this case, the cell radius will be 2. ks, kb, kal, kag, kv specify the elastic properties: stretching, bending, local area conservation, global area conservation and volume conservation respectively. These properties are described in Object-in-fluid interactions.

cell = OifCell(cellType=cell_type, partType=0, origin=[5.0, 5.0, 3.0])

Next, an actual object is created and its initial position is saved to a .vtk file (the directory output/sim1 needs to exist before the script is executed). Each object has to have a unique ID, specified using the keyword partType. The IDs have to start at 0 and increase consecutively. The other two mandatory arguments are cellType and origin. cellType specifies which previously defined cell type will be used for this object. origin gives placement of object’s center in the simulation box.

18.5.2.2. Specification of fluid and movement

lbf = espressomd.lb.LBFluidWalberla(agrid=1, density=1.0, kinematic_viscosity=1.5,
                                    tau=time_step, ext_force_density=[0.002, 0.0, 0.0])
self.system.lb = lbf

This part of the script specifies the fluid that will get the system moving. Here agrid \(=\Delta x\) is the spatial discretisation step, tau is the time step that will be the same as the time step for particles, viscosity viscosity and density density of the fluid are physical parameters scaled to lattice units, ext_force_density sets the force-per-unit-volume vector that drives the fluid. Another option to add momentum to fluid is by specifying the velocity on the boundaries.

Here we achieved the movement of the fluid by applying external force. Another alternative is to set up a wall/rhomboid with velocity. This does not mean that the physical boundary is moving, but rather that it transfers specified momentum onto the fluid.

18.5.2.3. Specification of boundaries

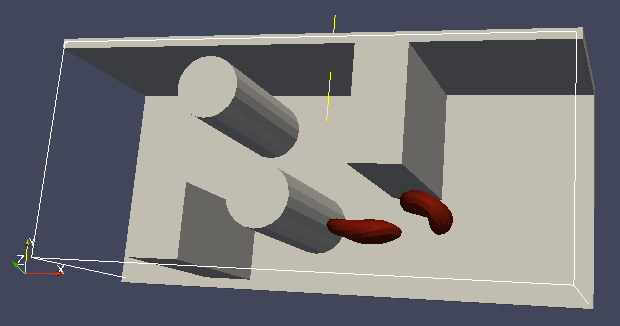
To set up the geometry of the channels, we mostly use rhomboids and cylinders, but there are also other shape types available in ESPResSo. Their usage is described elsewhere.

Each wall and obstacle has to be specified separately as a fluid boundary and as a particle constraint. The former enters the simulation as a boundary condition for the fluid, the latter serves for particle-boundary interactions. Sample cylinder and rhomboid can then be defined as follows. First we define the two shapes:

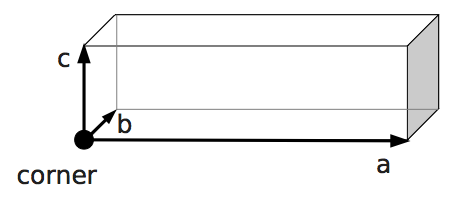
boundary1 = shapes.Rhomboid(corner=[0.0, 0.0, 0.0],
                            a=[boxX, 0.0, 0.0],
                            b=[0.0, boxY, 0.0],
                            c=[0.0, 0.0, 1.0],
                            direction=1)
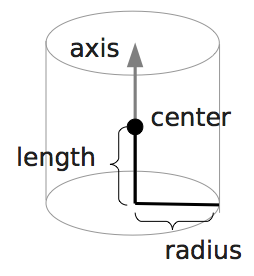
boundary2 = shapes.Cylinder(center=[11.0, 2.0, 7.0],
                            axis=[0.0, 0.0, 1.0],
                            length=7.0,
                            radius=2.0,
                            direction=1)

The direction=1 determines that the fluid is on the outside. Next we mark the LB nodes within the shapes as boundaries:

lbf.add_boundary_from_shape(boundary1)
lbf.add_boundary_from_shape(boundary2)

Followed by creating the constraints for cells:

system.constraints.add(shape=boundary1, particle_type=10)
system.constraints.add(shape=boundary2, particle_type=10)

The particle_type=10 will be important for specifying cell-wall interactions later. And finally, we output the boundaries for visualisation:

output_vtk_rhomboid(corner=[0.0, 0.0, 0.0],
                    a=[boxX, 0.0, 0.0],
                    b=[0.0, boxY, 0.0],
                    c=[0.0, 0.0, 1.0],
                    out_file="output/sim1/wallBack.vtk")
output_vtk_cylinder(center=[11.0, 2.0, 7.0],
                    axis=[0.0, 0.0, 1.0],
                    length=7.0,
                    radius=2.0,
                    n=20,
                    out_file="output/sim1/obstacle.vtk")

Note that the method for cylinder output also has an argument n. This specifies number of rectangular faces on the side.

It is a good idea to output and visualize the boundaries and objects just prior to running the actual simulation, to make sure that the geometry is correct and no objects intersect with any boundaries.

18.5.2.4. Specification of interactions

We can define an interaction with the boundaries:

system.non_bonded_inter[0, 10].soft_sphere.set_params(
    soft_a=0.0001, soft_n=1.2, soft_cut=0.1, soft_offset=0.0)

These interactions are also pointwise, e.g. each particle of type 0 (that means all mesh points of cell) will have a repulsive soft-sphere interaction with all boundaries of type 10 (here all boundaries) once it gets closer than soft_cut. The parameters soft_a and soft_n adjust how strong the interaction is and soft_offset is a distance offset, which will always be zero for our purposes.

18.5.2.5. System integration

And finally, the heart of this script is the integration loop at the end:

for i in range(1, 101):
    system.integrator.run(steps=500)
    cell.output_vtk_pos_folded(filename=f"output/sim1/cell_{i}.vtk")
    print(f"time: {i * time_step}")
print("Simulation completed.")

This simulation runs for 100 cycles. In each cycle, 500 integration steps are performed and output is saved into files output/sim1/cell_*.vtk. Note that they differ only by the number before the .vtk extension (this variable changes due to the for loop) and this will allow us to animate them in the visualisation software. str changes the type of i from integer to string, so that it can be used in the filename. The strings can be joined together by the + sign. Also, in each pass of the loop, the simulation time is printed in the terminal window and when the integration is complete, we should get a message about it.

To sum up, the proper order of setting up individual simulation parts is as follows:

• cell types

• cells

• fluid

• fluid boundaries

• interactions

If cell types and cells are specified after the fluid, the simulation is slower. Also, interactions can only be defined once the objects and boundaries both exist. Technically, the fluid boundaries can be specified before fluid, but it is really not recommended.

18.5.2.6. Running the simulation

The script can be executed in the terminal with

../pypresso script.py

Here script.py is the name of the script we just went over and ../pypresso should be replaced with the path to your executable. This command assumes that we are currently in the same directory as the script. Once the command is executed, messages should appear on the terminal about the creation of cell type, cell and the integration steps.

18.5.2.7. Writing out data

In the script, we have used the commands such as

cell.output_vtk_pos_folded(filename=f"output/sim1/cell_{i}.vtk")

to output the information about cell in every pass of the simulation loop. These files can then be used for inspection in ParaView and creation of animations. It is also possible to save a .vtk file for the fluid. And obviously, one can save various types of other data into text or data files for further processing and analysis.

18.5.3. Visualization in ParaView

For visualization we suggest the free software ParaView [5]. All .vtk files (boundaries, fluid, objects at all time steps) can be loaded at the same time. The loading is a two step process, because only after pressing the Apply button, are the files actually imported. Using the eye icon to the left of file names, one can turn on and off the individual objects and/or boundaries.

Fluid can be visualized using Filters/Alphabetical/Glyph (or other options from this menu. Please, refer to the ParaView user’s guide for more details).

Note, that ParaView does not automatically reload the data if they have been changed in the input folder, but a useful thing to know is that the created filters can be “recycled”. Once you delete the old data, load the new data and right-click on the existing filters, you can re-attach them to the new data.

It is a good idea to output and visualize the boundaries and objects just prior to running the actual simulation, to make sure that the geometry is correct and no objects intersect with any boundaries. This would cause “particle out of range” error and crash the simulation.

18.5.3.1. File format

ParaView (download at https://www.paraview.org) accepts .vtk files. For our cells we use the following format:

# vtk DataFile Version 3.0
Data
ASCII
DATASET POLYDATA
POINTS 393 float
p0x p0y p0z
p1x p1y p1z
...
p391x p391y p391z
p392x p392y p392z
TRIANGLE_STRIPS num_triang 4*num_triang
3 p1 p2 p3
3 p1 p3 p5
...
3 p390 p391 p392

where the cell has 393 surface nodes (particles). After initial specification, the list of points is present, with x, y, z coordinates for each. Then we write the triangulation, since that is how our surface is specified. We need to know the number of triangles (num_triang) and the each line/triangle is specified by 4 numbers (so we are telling ParaView to expect 4 * num_triang  numbers in the following lines. Each line begins with 3 (which stands for a triangle) and three point IDs that tell us which three points (from the order above) form this specific triangle.

18.5.3.2. Color coding of scalar data by surface points

It is possible to save (and visualize) data corresponding to individual surface points. These data can be scalar or vector values associated with all surface points. At the end of the .vtk file above, add the following lines:

POINT_DATA 393
SCALARS sample_scalars float 1
LOOKUP_TABLE default
value-at-p0
value-at-p1
...
value-at-p392

This says that data for each of 393 points are coming. Next line says that the data are scalar in this case, one float for each point. To color code the values in the visualization, a default (red-to-blue) table will be used. It is also possible to specify your own lookup table. As an example, we might want to see a force magnitude in each surface node

Stretched sphere after some relaxation, showing magnitude of total stretching force in each node.

18.5.3.3. Color coding of scalar data by triangles

It is also possible to save (and visualize) data corresponding to individual triangles

Red blood cell showing which triangles (local surface areas) are under most strain in shear flow.

In such case, the keyword POINT_DATA is changed to CELL_DATA and the number of triangles is given instead of number of mesh points.

# vtk DataFile Version 3.0
Data
ASCII
DATASET POLYDATA
POINTS 4 float
1 1 1
3 1 1
1 3 1
1 1 3
TRIANGLE_STRIPS 3 12
3 0 1 2
3 0 2 3
3 0 1 3
CELL_DATA 3
SCALARS sample_scalars float 1
LOOKUP_TABLE default
0.0
0.5
1.0

Note - it is also possible to save (and visualize) data corresponding to edges.

18.5.3.4. Multiple scalar data in one .vtk file

If one wants to switch between several types of scalar values corresponding to mesh nodes, these are specifies consecutively in the .vtk file, as follows. Their names (scalars1 and scalars2 in the following example) appear in a drop-down menu in ParaView.

POINT_DATA 393
SCALARS scalars1 float 1
LOOKUP_TABLE default
value1-at-p0
value1-at-p1
...
value1-at-p392
SCALARS scalars2 float 1
LOOKUP_TABLE default
value2-at-p0
value2-at-p1
...
value2-at-p392

18.5.3.5. Vector data for objects .vtk file

If we want to observe some vector data (e.g. outward normal, fig. [fig:vectordata]) at points of the saved objects, we can use the following structure of the .vtk file, where the vector at one point is [v1, v2, v3]:

POINT_DATA 393
VECTORS vector_field float
v1-at-p0 v2-at-p0 v3-at-p0
v1-at-p1 v2-at-p1 v3-at-p1
...
v1-at-p391 v2-at-p391 v3-at-p392

Example of vector data stored in points of the object

More info on .vtk files and possible options:

https://vtk.org/wp-content/uploads/2015/04/file-formats.pdf

18.5.3.6. Automatic loading

Sometimes it is frustrating to reload data in ParaView: manually open all the files, click all the properties etc. This however, can be done automatically.

Scenario:

Load file data.vtk with the fluid velocity field.

Add filter called slice to visualize the flow field on the cross-section.

To do it automatically, ParaView has a feature for tracking steps. To record the steps that create the scenario above, first choose Tools/Start Trace. From that moment, all the steps done in ParaView will be recorded. Then you Tools/Stop Trace. Afterwards, a window appears with a python code with recorded steps. It needs to be saved as, e.g. loading-script.py.

Next time you open ParaView with command paraview --script=loading-script.py and all the steps for creating that scenario will be executed and you end up with the velocity field visualized.

18.5.4. Available Object-in-fluid (OIF) classes

Here we describe the currently available OIF classes and commands. Note that there are more still being added. We would be pleased to hear from you about any suggestions on further functionality.

Notation: keywords, parameter values, vectors

The keywords do not have to be in a specific order.

18.5.4.1. class OifCellType

For those familiar with earlier version of object-in-fluid framework, this class corresponds to the oif_emplate in tcl. It contains a “recipe” for creating cells of the same type. These cells can then be placed at different locations with different orientation, but their elasticity and size is determined by the CellType. There are no actual particles created at this stage. Also, while the interactions are defined, no bonds are created here.

OifCellType.print_info()
OifCellType.mesh.output_mesh_triangles(filename)

nodesfile=nodes.dat - input file. Each line contains three real numbers. These are the x, y, z coordinates of individual surface mesh nodes of the objects centered at [0,0,0] and normalized so that the “radius” of the object is 1.

trianglesfile=triangles.dat - input file. Each line contains three integers. These are the ID numbers of the mesh nodes as they appear in nodes.dat. Note that the first node has ID 0.

system=system Particles of cells created using this template will be added to this system. Note that there can be only one system per simulation.

ks=value - elastic modulus for stretching forces.

kslin= value - elastic modulus for linear stretching forces.

kb= value - elastic modulus for bending forces.

kal= value - elastic modulus for local area forces.

The switches ks, kb and kal set elastic parameters for local interactions: ks for edge stiffness, kb for angle preservation stiffness and kal for triangle area preservation stiffness. Currently, the stiffness is implemented to be uniform over the whole object, but with some tweaking, it is possible to have non-uniform local interactions.

Note, the difference between stretching (ks) and linear stretching (kslin) - these two options cannot be used simultaneously:

Linear stretching behaves like linear spring, where the stretching force is calculated as \(\mathbf{F}_s=k_s*\Delta L\), where \(\Delta L\) is the prolongation of the given edge. By default, the stretching is non-linear (neo-Hookian).

kvisc=value - elastic modulus for viscosity of the membrane. Viscosity slows down the reaction of the membrane.

kag=value - elastic modulus for global area forces

kv=value - elastic modulus for volume forces

Note: At least one of the elastic moduli should be set.

resize=(x, y, z) - coefficients, by which the coordinates stored in nodesfile will be stretched in the x, y, z direction. The default value is (1.0, 1.0, 1.0).

mirror=(x, y, z) - whether the respective coordinates should be flipped around 0. Arguments x, y, z must be either 0 or 1. The reflection of only one coordinate is allowed so at most one argument is set to 1, others are 0. For example mirror=(0, 1, 0) results in flipping the coordinates (x, y, z) to (x, -y, z). The default value is (0, 0, 0).

normal - by default set to False, however without this option enabled, the membrane collision (and thus cell-cell interactions) will not work.

check_orientation - by default set to True. This options performs a check, whether the supplied trianglesfile contains triangles with correct orientation. If not, it corrects the orientation and created cells with corrected triangles. It is useful for new or unknown meshes, but not necessary for meshes that have already been tried out. Since it can take a few minutes for larger meshes (with thousands of nodes), it can be set to False. In that case, the check is skipped when creating the CellType and a warning is displayed.

The order of indices in triangles.dat is important. Normally, each triangle ABC should be oriented in such a way, that the normal vector computed as vector product ABxAC must point inside the object. For example, a sphere (or any other sufficiently convex object) contains such triangles that the normals of these triangles point towards the center of the sphere (almost).

The check runs over all triangles, makes sure that they have the correct orientation and then calculates the volume of the object. If the result is negative, it flips the orientation of all triangles.

Note, this method tells the user about the correction it makes. If there is any, it might be useful to save the corrected triangulation for future simulations using the method CellType.mesh.OutputMeshTriangles(filename), so that the check does not have to be used repeatedly.

CellType.mesh.output_mesh_triangles(filename) - this is useful after checking orientation, if any of the triangles where corrected. This method saves the current triangles into a file that can be used as input in the next simulations.

CellType.print_info() - prints the information about the template.

18.5.4.2. class OifCell

OifCell.set_origin([x, y, z])
OifCell.get_origin()
OifCell.get_origin_folded()
OifCell.get_approx_origin()
OifCell.get_velocity()
OifCell.set_velocity([x, y, z])
OifCell.pos_bounds()
OifCell.surface()
OifCell.volume()
OifCell.diameter()
OifCell.get_n_nodes()
OifCell.set_force([x, y, z])
OifCell.kill_motion()
OifCell.unkill_motion()
OifCell.output_vtk_pos(filename.vtk)
OifCell.output_vtk_pos_folded(filename.vtk)
OifCell.append_point_data_to_vtk(filename.vtk, dataname, data, firstAppend)
OifCell.output_raw_data(filename, rawdata)
OifCell.output_mesh_points(filename)
OifCell.set_mesh_points(filename)
OifCell.elastic_forces(elasticforces, fmetric, vtkfile, rawdatafile)
OifCell.print_info()

cell_type - object will be created using nodes, triangle incidences, elasticity parameters and initial stretching saved in this cellType.

part_type=type - must start at 0 for the first cell and increase consecutively for different cells. Volume calculation of individual objects and interactions between objects are set up using these types.

origin=(x, y, z) - center of the object will be at this point.

rotate=(x, y, z) - angles in radians, by which the object will be rotated about the x, y, z axis. Default value is (0.0, 0.0, 0.0). Value (\(\pi/2, 0.0, 0.0\)) means that the object will be rotated by \(\pi/2\) radians clockwise around the x axis when looking in the positive direction of the axis.

mass=m - mass of one particle. Default value is 1.0.

OifCell.set_origin(o) - moves the object such that the origin has coordinates o=(x, y, z).

OifCell.get_origin() - outputs the location of the center of the object.

OifCell.get_origin_folded() - outputs the location of the center of the object. For periodical movements the coordinates are folded (always within the computational box).

OifCell.get_approx_origin() - outputs the approximate location of the center of the object. It is computed as average of 6 mesh points that have extremal x, y and z coordinates at the time of object loading.

OifCell.get_velocity() - outputs the average velocity of the object. Runs over all mesh points and outputs their average velocity.

OifCell.set_velocity(v) - sets the velocities of all mesh points to v=(\(v_x\), \(v_y\), \(v_z\)).

OifCell.pos_bounds() - computes six extremal coordinates of the object. More precisely, runs through the all mesh points and returns the minimal and maximal \(x\)-coordinate, \(y\)-coordinate and \(z\)-coordinate in the order (\(x_{max}\), \(x_{min}\), \(y_{max}\), \(y_{min}\), \(z_{max}\), \(z_{min}\)).

OifCell.surface() - outputs the surface of the object.

OifCell.volume() - outputs the volume of the object.

OifCell.diameter() - outputs the largest diameter of the object.

OifCell.get_n_nodes() - returns the number of mesh nodes.

OifCell.set_force(f) - sets the external force vector f=(\(f_x\), \(f_y\), \(f_z\)) to all mesh nodes of the object. Setting is done using command p.set_force(f). Note, that this command sets the external force in each integration step. So if you want to use the external force only in one iteration, you need to set zero external force in the following integration step.

OifCell.kill_motion() - stops all the particles in the object (analogue to the command p.kill_motion()).

OifCell.unkill_motion() - enables the movement of all the particles in the object (analogue to the command p.unkill_motion()).

OifCell.output_vtk_pos(filename.vtk) - outputs the mesh of the object to the desired filename.vtk. ParaView can directly visualize this file.

OifCell.output_vtk_pos_folded(filename.vtk) - outputs the mesh of the object to the desired filename.vtk. ParaView can directly visualize this file. For periodical movements the coordinates are folded (always within the computational box).

OifCell.append_point_data_to_vtk(filename.vtk, dataname, data, firstAppend) - outputs the specified scalar data to an existing filename.vtk. This is useful for ParaView visualisation of local velocity magnitudes, magnitudes of forces, etc. in the meshnodes and can be shown in ParaView by selecting the dataname in the Properties toolbar. It is possible to consecutively write multiple datasets into one filename.vtk. For the first one, the firstAppend parameter is set to True, for the following datasets, it needs to be set to False. This is to ensure the proper structure of the output file.

OifCell.output_raw_data(filename, rawdata) - outputs the vector rawdata about the object into the filename.

OifCell.output_mesh_points(filename) - outputs the positions of the mesh nodes to filename. In fact, this command creates a new nodes.dat file that can be used by the method OifCell.set_mesh_points(nodes.dat). The center of the object is located at point (0.0, 0.0, 0.0). This command is aimed to store the deformed shape in order to be loaded later.

OifCell.set_mesh_points(filename) - deforms the object in such a way that its origin stays unchanged, however the relative positions of the mesh points are taken from file filename. The filename should contain the coordinates of the mesh points with the origin location at (0.0, 0.0, 0.0). The procedure also checks whether number of lines in the filename is the same as the corresponding value from OifCell.get_n_nodes().

OifCell.elastic_forces(elasticforces, fmetric, vtkfile, rawdatafile) - this method can be used in two different ways. One is to compute the elastic forces locally for each mesh node and the other is to compute the f-metric, which is an approximation of elastic energy.

To compute the elastic forces, use the vector elasticforces. It is a sextuple of zeros and ones, e.g. elasticforces = (1,0,0,1,0,0), where the ones denote the elastic forces to be computed. The order is (stretching, bending, local area, global area, volume, total). The output can be saved in two different ways: either by setting vtkfile = filename.vtk, which saves a .vtk file that can be visualized using ParaView. If more than one elastic force was selected, they can be chosen in the Properties window in ParaView. The other type of output is rawdatafile=filename.dat, which will save a datafile with the selected type of elastic force - one force per row, where each row corresponds to a single mesh node. Note that only one type of elastic force can be written this way at a time. Thus, if you need output for several elastic forces, this method should be called several times.

To compute the f-metric, use the vector fmetric. It is again a sextuple of zeros and ones, e.g. fmetric = (1,1,0,0,0,0), where the ones denote the elastic forces to be computed. The order is (stretching, bending, local area, global area, volume, total). The output is again a vector with six elements, each corresponding to the requested f-metric/“naive energy” computed as a sum of magnitudes of respective elastic forces over all nodes of the object.

OifCell.print_info() - prints the information about the elastic object.

18.5.4.3. Short utility procedures

get_n_triangle(a, b, c) - returns the normal n to the triangle given by points (a, b, c).

norm(v) - returns the norm of the vector v.

distance(a, b) - returns the distance between points a and b.

area_triangle(a, b, c) - returns the area of the given triangle (a, b, c).

angle_btw_triangles(\(\mathbf{p}_1\), \(\mathbf{p}_2\), \(\mathbf{p}_3\), \(\mathbf{p}_4\) - returns the angle \(\phi\) between two triangles: (\(\mathbf{p}_1\), \(\mathbf{p}_2\), \(\mathbf{p}_3\)) and (\(\mathbf{p}_3\), \(\mathbf{p}_2\), \(\mathbf{p}_4\)) that have a common edge (\(\mathbf{p}_2\), \(\mathbf{p}_3\)).

discard_epsilon(x) - needed for rotation; discards very small numbers x.

oif_neo_hookean_nonlin(\(\lambda\)) - nonlinearity for neo-Hookean stretching

calc_stretching_force(\(k_s,\ \mathbf{p}_A,\ \mathbf{p}_B\), dist0, dist) - computes the nonlinear stretching force with given \(k_s\) for points \(\mathbf{p}_A\) and \(\mathbf{p}_B\) given by their coordinates, whose initial distance was dist0 and current distance is dist.

calc_linear_stretching_force(\(k_s,\ \mathbf{p}_A,\ \mathbf{p}_B\), dist0, dist) - computes the linear stretching force with given \(k_s\) for points \(\mathbf{p}_A\) and \(\mathbf{p}_B\) given by their coordinates, whose initial distance was dist0 and current distance is dist.

calc_bending_force(\(k_b,\ \mathbf{p}_A,\ \mathbf{p}_B,\ \mathbf{p}_C,\ \mathbf{p}_D,\ \phi_0,\ \phi\)) - computes the bending force with given \(k_b\) for points \(\mathbf{p}_A\), \(\mathbf{p}_B\), \(\mathbf{p}_C\) and \(\mathbf{p}_D\) (\(\triangle_1\)=BAC; \(\triangle_2\)=BCD) given by their coordinates; the initial angle for these two triangles was \(\phi_0\), the current angle is \(\phi\).

calc_local_area_force(\(k_{al},\ \mathbf{p}_A,\ \mathbf{p}_B,\ \mathbf{p}_C,\ A_0,\ A\)) - computes the local area force with given \(k_{al}\) for points \(\mathbf{p}_A\), \(\mathbf{p}_B\) and \(\mathbf{p}_C\) given by their coordinates; the initial area of triangle ABC was \(A_0\), the current area is \(A\).

calc_global_area_force(\(k_{ag},\ \mathbf{p}_A,\ \mathbf{p}_B,\ \mathbf{p}_C,\ A_{g0},\ A_g\)) - computes the global area force with given \(k_{ag}\) for points \(\mathbf{p}_A\), \(\mathbf{p}_B\) and \(\mathbf{p}_C\) given by their coordinates; the initial surface area of the object was \(A_{g0}\), the current surface area of the object is \(A_g\).

calc_volume_force(\(k_v,\ \mathbf{p}_A,\ \mathbf{p}_B,\ \mathbf{p}_C,\ V_0,\ V\)) - computes the volume force with given \(k_v\) for points \(\mathbf{p}_A\), \(\mathbf{p}_B\) and \(\mathbf{p}_C\) given by their coordinates; the initial volume of the object was \(V_0\), the current volume of the object is \(V\).

output_vtk_rhomboid(corner, a, b, c, outFile.vtk) - outputs rhomboid boundary for later visualisation in ParaView.

output_vtk_cylinder(center, normal, L, r, n, outFile.vtk) - outputs cylinder boundary for later visualisation in ParaView.

output_vtk_lines(lines, outFile.vtk) - outputs a set of line segments for later visualisation in ParaView.

18.5.4.4. Description of helper classes

Awareness of these classes is not necessary for a user of OIF module, but is essential for developers who wish to modify it because it shows how the object data are stored.

classes FixedPoint and PartPoint

Class PartPoint represents a particle. These particles are then used as building blocks for edges, angles, triangles and ultimately the whole object mesh. Since we use a two-step process to create the objects, it is necessary to distinguish between a FixedPoint and PartPoint. FixedPoint is a point used by template and does not correspond to particle. The FixedPoints of one OifCellType form a mesh that is centered around origin. Only after it is stretched and shifted to the object origin are the PartPoints of the given object created.

classes Edge, Angle, Triangle, ThreeNeighbors

These classes represent the building blocks of a mesh. They are used to compute the elastic interactions: Edge is for stretching, Angle for bending, Triangle for local and global area and volume and ThreeNeigbors for calculation of outward normal vector needed for cell-cell interaction.

class Mesh

This class holds all the information about the geometry of the object, including nodes, edges, angles, triangles and neighboring points. The mesh of OifCellType is copied every time a new object (i.e. OifCell) of this type is created. This saves computational time, since the data for elastic interactions of the given object do not need to be recalculated every time.

[5]

https://www.paraview.org/

18.6. Particle polarizability with thermalized cold Drude oscillators

Note

Requires features THOLE, P3M, THERMOSTAT_PER_PARTICLE.

Note

Drude is only available for the P3M electrostatics solver and the Langevin thermostat.

Thermalized cold Drude oscillators can be used to simulate polarizable particles. The basic idea is to add a ‘charge-on-a-spring’ (Drude charge) to a particle (Drude core) that mimics an electron cloud which can be elongated to create a dynamically inducible dipole. The energetic minimum of the Drude charge can be obtained self-consistently, which requires several iterations of the system’s electrostatics and is usually considered computationally expensive. However, with thermalized cold Drude oscillators, the distance between Drude charge and core is coupled to a thermostat so that it fluctuates around the SCF solution. This thermostat is kept at a low temperature compared to the global temperature to minimize the heat flow into the system. A second thermostat is applied on the centre of mass of the Drude charge + core system to maintain the global temperature. The downside of this approach is that usually a smaller time step has to be used to resolve the high frequency oscillations of the spring to get a stable system.

In ESPResSo, the basic ingredients to simulate such a system are split into three bonds:

1. A Harmonic bond to account for the spring.

2. A Thermalized distance bond with a cold thermostat on the Drude-Core distance.

3. A Subtract P3M short-range bond to cancel the electrostatic interaction between Drude and core particles.

The system-wide thermostat has to be applied to the centre of mass and not to the core particle directly. Therefore, the particles have to be excluded from global thermostatting. With THERMOSTAT_PER_PARTICLE enabled, we set the friction coefficient of the Drude complex to zero.

As the Drude charge should not alter the charge or mass of the Drude complex, both properties have to be subtracted from the core when adding the Drude particle. In the following convention, we assume that the Drude charge is always negative. It is calculated via the spring constant \(k\) and polarizability \(\alpha\) (in units of inverse volume) with \(q_d = -\sqrt{k \cdot \alpha}\).

The following helper method takes into account all the preceding considerations and can be used to conveniently add a Drude particle to a given core particle. It returns a ParticleHandle of the created Drude particle. Note that as the function also adds the first two bonds between Drude and core, these bonds have to be already available.

import espressomd.drude_helpers
dh = espressomd.drude_helpers.DrudeHelpers()
drude_part = dh.add_drude_particle_to_core(<system>, <harmonic_bond>,
    <thermalized_bond>, <core particle>, <type drude>, <alpha>,
    <mass drude>, <coulomb_prefactor>, <thole damping>, <verbose>)

The arguments of the helper function are:

• <system>: The espressomd.System().

• <harmonic_bond>: The harmonic bond of the charge-on-a-spring. This is added between core and newly generated Drude particle

• <thermalized_bond>: The thermalized distance bond for the cold and hot thermostats.

• <core particle>: The core particle on which the Drude particle is added.

• <type drude>: The user-defined type of the Drude particle. Each Drude particle of each complex should have an individual type (e.g. in an ionic system with Anions (type 0) and Cations (type 1), two new, individual Drude types have to be assigned).

• <alpha>: The polarizability volume.

• <coulomb_prefactor>: The Coulomb prefactor of the system. Used to calculate the Drude charge from the polarizability and the spring constant of the Drude bond.

• <thole damping>: (optional) An individual Thole damping parameter for the core-Drude pair. Only relevant if Thole damping is used (defaults to 2.6).

• <verbose>: (bool, optional) Prints out information about the added Drude particles (default: False)

What is still missing is the short-range exclusion bond between all Drude-core pairs. One bond type of this kind is needed per Drude type. The above helper function also tracks particle types, ids and charges of Drude and core particles, so a simple call of another helper function:

dh.setup_and_add_drude_exclusion_bonds(system)

will use this data to create a Subtract P3M short-range bond per Drude type and set it up it between all Drude and core particles collected in calls of add_drude_particle_to_core().

18.6.1. Canceling intramolecular electrostatics

Note that for polarizable molecules (i.e. connected particles, coarse grained models etc.) with partial charges on the molecule sites, the Drude charges will have electrostatic interaction with other cores of the molecule. Often, this is unwanted, as it might be already part of the force-field (via. partial charges or parametrization of the covalent bonds). Without any further measures, the elongation of the Drude particles will be greatly affected be the close-by partial charges of the molecule. To prevent this, one has to cancel the interaction of the Drude charge with the partial charges of the cores within the molecule. This can be done with special bonds that subtracts the P3M short-range interaction of the charge portion \(q_d q_{partial}\). This ensures that only the dipolar interaction inside the molecule remains. It should be considered that the error of this approximation increases with the share of the long-range part of the electrostatic interaction. Two helper methods assist with setting up this exclusion. If used, they have to be called after all Drude particles are added to the system:

espressomd.drude_helpers.setup_intramol_exclusion_bonds(<system>, <molecule drude types>,
    <molecule core types>, <molecule core partial charges>, <verbose>)

This function creates the required number of bonds which are later added to the particles. It has to be called only once. In a molecule with \(N\) polarizable sites, \(N \cdot (N-1)\) bond types are needed to cover all the combinations. Parameters are:

• <system>: The espressomd.System().

• <molecule drude types>: List of the Drude types within the molecule.

• <molecule core types>: List of the core types within the molecule that have partial charges.

• <molecule core partial charges>: List of the partial charges on the cores.

• <verbose>: (bool, optional) Prints out information about the created bonds (default: False)

After setting up the bonds, one has to add them to each molecule with the following method:

espressomd.drude_helpers.add_intramol_exclusion_bonds(<system>, <drude ids>, <core ids>, <verbose>)

This method has to be called for all molecules and needs the following parameters:

• <system>: The espressomd.System().

• <drude ids>: The ids of the Drude particles within one molecule.

• <core ids>: The ids of the core particles within one molecule.

• <verbose>: (bool, optional) Prints out information about the added bonds (default: False)

Internally, this is done with the bond described in Subtract P3M short-range bond, that simply adds the p3m shortrange pair-force of scale \(- q_{\textrm{d}} q_{\textrm{partial}}\) the to bonded particles.

See also

Often used in conjunction with Drude oscillators is the Thole correction to damp dipole-dipole interactions on short distances. It is available in ESPResSo as a non-bonded interaction.