Tutorial 5: Raspberry Electrophoresis

1 Tutorial Outline

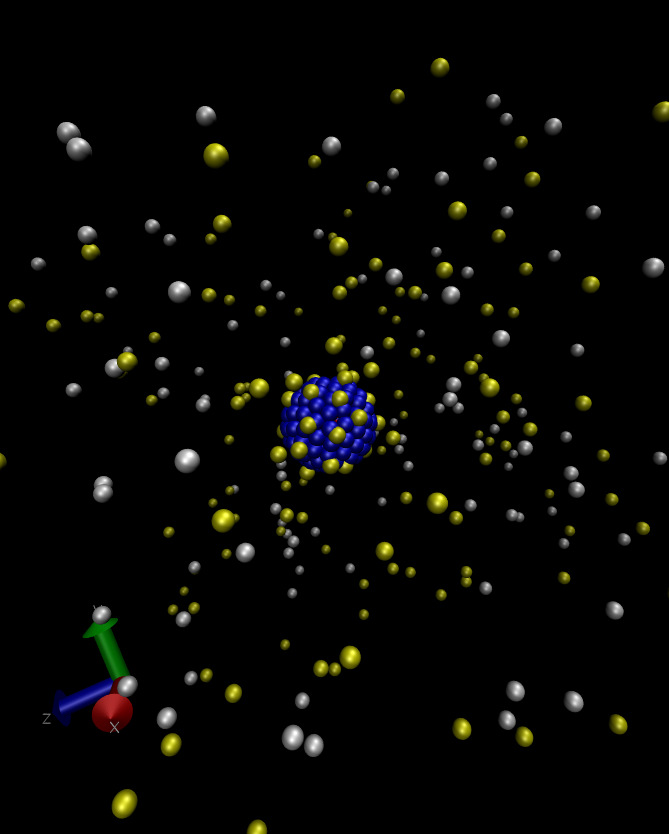
Welcome to the raspberry electrophoresis ESPResSo tutorial! This tutorial assumes some basic knowledge of ESPResSo. The first step is compiling ESPResSo with the appropriate flags, as listed in Sec. 2. The tutorial starts by discussing how to build a colloid out of a series of MD beads. These particles typically resemble a raspberry as can be seen in Fig. 1. After covering the construction of a raspberry colloid, we then briefly discuss the inclusion of hydrodynamic interactions via a lattice-Boltzmann fluid. Finally we will cover including ions via the restrictive primitive model (hard sphere ions) and the addition of an electric field to measure the electrokinetic properties. This script will run a raspberry electrophoresis simulation and write the time and position of the colloid out to a file named posVsTime.dat in the same directory. A sample set of data is included in the file posVsTime_sample.dat.

2 Compiling ESPResSo for this Tutorial

The first thing to do with any ESPResSo project is to compile ESPResSo with all of the necessary features. The following myconfig.hpp example contains all of the flags needed for running the accompanying Python script. Please compile ESPResSo using this myconfig.hpp before starting this tutorial.

#define ELECTROSTATICS
#define ROTATION
#define ROTATIONAL_INERTIA
#define EXTERNAL_FORCES
#define MASS
#define VIRTUAL_SITES_RELATIVE
#define LENNARD_JONES

3 Global MD Variables

The first thing to do in any ESPResSo simulation is to import our espressomd features and set a few global simulation parameters:

The parameter box_l sets the size of the simulation box. In general, one should check for finite size effects which can be surprisingly large in simulations using hydrodynamic interactions. They also generally scale as box_l$^{-1}$ or box_l$^{-3}$ depending on the transport mechanism which sometimes allows for the infinite box limit to be extrapolated to, instead of using an excessively large simulation box. As a rule of thumb, the box size should be five times greater than the characteristic length scale of the object. Note that this example uses a small box to provide a shorter simulation time.

The skin is used for constructing the Verlet lists and is purely an optimization parameter. Whatever value provides the fastest integration speed should be used. For the type of simulations covered in this tutorial, this value turns out to be skin$\ \approx 0.3$.

The periodicity parameter indicates that the system is periodic in all three dimensions. Note that the lattice-Boltzmann algorithm requires periodicity in all three directions (although this can be modified using boundaries, a topic not covered in this tutorial).

4 Setting up the Raspberry

Setting up the raspberry is a non-trivial task. The main problem lies in creating a relatively uniform distribution of beads on the surface of the colloid. In general one should take about 1 bead per lattice-Boltzmann grid point on the surface to ensure that there are no holes in the surface. The behavior of the colloid can be further improved by placing beads inside the colloid, though this is not done in this example script. In our example we first define a harmonic interaction causing the surface beads to be attracted to the center, and a Lennard-Jones interaction preventing the beads from entering the colloid. There is also a Lennard-Jones potential between the surface beads to get them to distribute evenly on the surface.

We set up the central bead and the other beads are initialized at random positions on the surface of the colloid. The beads are then allowed to relax using an integration loop where the forces between the beads are capped.

The best way to ensure a relatively uniform distribution of the beads on the surface is to simply take a look at a VMD snapshot of the system after this integration. Such a snapshot is shown in Fig. 1.

missing
Figure 1: A snapshot of the simulation consisting of positive salt ions (yellow spheres), negative salt ions (grey spheres) and surface beads (blue spheres). There is also a central bead in the middle of the colloid bearing a large negative charge.

In order to make the colloid perfectly round, we now adjust the bead's positions to be exactly radius_col away from the central bead.

Now that the beads are arranged in the shape of a raspberry, the surface beads are made virtual particles using the VirtualSitesRelative scheme. This converts the raspberry to a rigid body in which the surface particles follow the translation and rotation of the central particle. Newton's equations of motion are only integrated for the central particle. It is given an appropriate mass and moment of inertia tensor (note that the inertia tensor is given in the frame in which it is diagonal.)

5 Inserting Counterions and Salt Ions

Next we insert enough ions at random positions (outside the radius of the colloid) with opposite charge to the colloid such that the system is electro-neutral. In addition, ions of both signs are added to represent the salt in the solution.

We then check that charge neutrality is maintained

A WCA potential acts between all of the ions. This potential represents a purely repulsive version of the Lennard-Jones potential, which approximates hard spheres of diameter $\sigma$. The ions also interact through a WCA potential with the central bead of the colloid, using an offset of around $\mathrm{radius\_col}-\sigma +a_\mathrm{grid}/2$. This makes the colloid appear as a hard sphere of radius roughly $\mathrm{radius\_col}+a_\mathrm{grid}/2$ to the ions, which is approximately equal to the hydrodynamic radius of the colloid

After inserting the ions, again a short integration is performed with a force cap to prevent strong overlaps between the ions.

6 Electrostatics

Electrostatics are simulated using the Particle-Particle Particle-Mesh (P3M) algorithm. In ESPResSo this can be added to the simulation rather trivially:

Generally a Bjerrum length of $2$ is appropriate when using WCA interactions with $\sigma=1$, since a typical ion has a radius of $0.35\ \mathrm{nm}$, while the Bjerrum length in water is around $0.7\ \mathrm{nm}$.

The external electric field is simulated by simply adding a constant force equal to the simulated field times the particle charge. Generally the electric field is set to $0.1$ in MD units, which is the maximum field before the response becomes nonlinear. Smaller fields are also possible, but the required simulation time is considerably larger. Sometimes, Green-Kubo methods are also used, but these are generally only feasible in cases where there is either no salt or a very low salt concentration.

7 Lattice-Boltzmann

Before creating the LB fluid it is a good idea to set all of the particle velocities to zero. This is necessary to set the total momentum of the system to zero. Failing to do so will lead to an unphysical drift of the system, which will change the values of the measured velocities.

The important parameters for the LB fluid are the density, the viscosity, the time step, and the friction coefficient used to couple the particle motion to the fluid. The time step should generally be comparable to the MD time step. While large time steps are possible, a time step of $0.01$ turns out to provide more reasonable values for the root mean squared particle velocities. Both density and viscosity should be around $1$, while the friction should be set around $20.$ The grid spacing should be comparable to the ions' size.

A logical way of picking a specific set of parameters is to choose them such that the hydrodynamic radius of an ion roughly matches its physical radius determined by the WCA potential ($R=0.5\sigma$). Using the following equation:

\begin{equation} \frac{1}{\Gamma}=\frac{1}{6\pi \eta R_{\mathrm{H0}}}=\frac{1}{\Gamma_0} +\frac{1}{g\eta a} \label{effectiveGammaEq} \end{equation}

one can see that the set of parameters grid spacing $a=1\sigma$, fluid density $\rho=1$, a kinematic viscosity of $\nu=3 $ and a friction of $\Gamma_0=50$ leads to a hydrodynamic radius of approximately $0.5\sigma$.

The last step is to first turn off all other thermostats, followed by turning on the LB thermostat. The temperature is typically set to 1, which is equivalent to setting $k_\mathrm{B}T=1$ in molecular dynamics units.

8 Simulating Electrophoresis

Now the main simulation can begin! The only important thing is to make sure the system has enough time to equilibrate. There are two separate equilibration times: 1) the time for the ion distribution to stabilize, and 2) the time needed for the fluid flow profile to equilibrate. In general, the ion distribution equilibrates fast, so the needed warmup time is largely determined by the fluid relaxation time, which can be calculated via $\tau_\mathrm{relax} = \mathrm{box\_length}^2/\nu$. This means for a box of size 40 with a kinematic viscosity of 3 as in our example script, the relaxation time is $\tau_\mathrm{relax} = 40^2/3 = 533 \tau_\mathrm{MD}$, or 53300 integration steps. In general it is a good idea to run for many relaxation times before starting to use the simulation results for averaging observables. To be on the safe side $10^6$ integration steps is a reasonable equilibration time. Please feel free to modify the provided script and try and get some interesting results!