The lattice-Boltzmann method in ESPResSo¶

Before you start:¶

With this tutorial you can get started using the lattice-Boltzmann method for hydrodynamics. We give a brief introduction about the theory and how to use the method in ESPResSo. We have selected two interesting problems for which LB can be applied and which are well understood. You can start with any of them. One is contained in this folder, and the other one can be found in the polymers tutorial folder. The latter tutorial is relatively long and working through it carefully will take at least a full day. You can however get a glimpse of different aspects by starting to work on the tasks.

Note: LB cannot be used as a black box. It is unavoidable to spend time learning the theory and gaining practical experience.

1 Introduction¶

In this tutorial, you will learn the basics of the lattice-Boltzmann method (LBM) with special focus on the application on soft matter simulations or more precisely on how to apply it in combination with molecular dynamics to take into account hydrodynamic solvent effects without the need to introduce thousands of solvent particles. The LBM – its theory as well as its applications – is a very active field of research with more than 30 years of development.

Tutorial Outline¶

This tutorial should enable you to start a scientific project applying the LB method with ESPResSo. In the first part we summarize a few basic ideas behind LB and describe the interface. In the second part we reproduce the flow profile of a fluid moving through a pipe under a homogeneous force density, which is known as Poiseuille flow. In the Polymer diffusion tutorial in the polymers folder the length dependence of the diffusion of polymers is analyzed.

Notes on the ESPResSo version you will need¶

ESPResSo offers both CPU and GPU support for LB. We recommend using the GPU code, as it is much (10x) faster than the CPU code. It should be noted, that the GPU code only uses single precision floating point numbers whereas the CPU code uses double precision. For most applications, however, single precision is sufficient.

For the tutorial you will have to compile in the following features:

#define LENNARD_JONES

Please uncomment the features in the myconfig.hpp and compile ESPResSo using this myconfig.hpp. This is not necessary if you do not use a custom myconfig.hpp, since the features are activated by default. For more information on configuring ESPResSo and how to activate CUDA (for GPU computation), refer to the documentation.

2 The LBM in brief¶

Linearized Boltzmann equation¶

Here we want to repeat a few very basic facts about the LBM. You will find much better introductions in various books and articles, e.g. [1, 2]. It will however help clarifying our choice of words and we will eventually say something about the implementation in ESPResSo. It is very loosely written, with the goal that the reader understands basic concepts and how they are implemented in ESPResSo.

The LBM essentially consists of solving a fully discretized version of the linearized Boltzmann equation. The Boltzmann equation describes the time evolution of the one particle distribution function $f \left(\vec{x}, \vec{p}, t\right)$, which is the probability of finding a molecule in a phase space volume $d^3\vec{x}\,d^3\vec{p}$ at time $t$. The function $f$ is normalized so that the integral over the whole phase space is the total mass of the particles:

$$\int \int f \left(\vec{x}, \vec{p}, t\right) \,d^3\vec{x}\,d^3\vec{p} = N,$$

where $N$ denotes the particle number. The quantity $f\left(\vec{x}, \vec{p}, t\right) \,d^3\vec{x}\,d^3\vec{p}$ corresponds to the number of particles in this particular cell of the phase space, the population.

Discretization¶

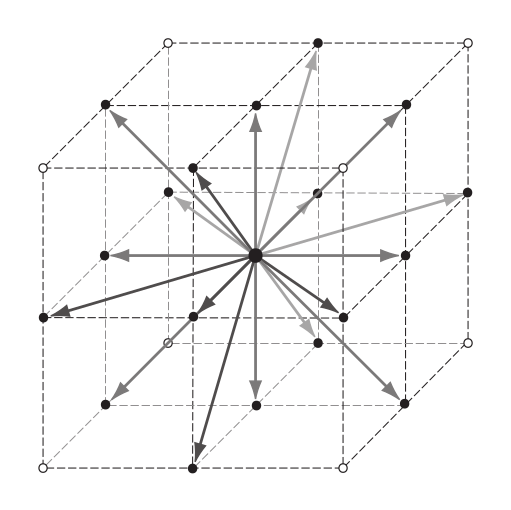
The LBM discretizes the Boltzmann equation not only in real space (the lattice!) and time, but also the velocity space is discretized. A surprisingly small number of velocities, usually 19 in 3D, is sufficient to describe incompressible, viscous flow correctly. Mostly we will refer to the three-dimensional model with a discrete set of 19 velocities, which is conventionally called D3Q19. These velocities, $\vec{c_i}$ , are chosen such that they correspond to the movement from one lattice node to another in one time step. A two step scheme is used to transport information through the system. In the streaming step the particles (in terms of populations) are transported to the cell where the corresponding velocity points to. In the collision step, the distribution functions in each cell are relaxed towards the local thermodynamic equilibrium. This will be described in more detail below.

The hydrodynamic fields, the density $\rho$, the fluid momentum density $\vec{j}$ and the pressure tensor $\Pi$ can be calculated straightforwardly from the populations. They correspond to the moments of the distribution function:

\begin{align*} \rho &= \sum_i f_i \\ \vec{j} = \rho \vec{u} &= \sum_i f_i \vec{c_i} \\ \Pi^{\alpha \beta} &= \sum_i f_i \vec{c_i}^{\alpha}\vec{c_i}^{\beta} \end{align*}

Here the Greek indices denotes the cartesian axis and the Latin indices indicate the number in the discrete velocity set. Note that the pressure tensor is symmetric. It is easy to see that these equations are linear transformations of the $f_i$ and that they carry the most important information. They are 10 independent variables, but this is not enough to store the full information of 19 populations. Therefore 9 additional quantities are introduced. Together they form a different basis set of the 19-dimensional population space, the modes space and the modes are denoted by $m_i$. The 9 extra modes are referred to as kinetic modes or ghost modes. It is possible to explicitly write down the base transformation matrix, and its inverse and in the ESPResSo LBM implementation this basis transformation is made for every cell in every LBM step.

The 19 velocity vectors $\vec{c_i}$ for a D3Q19 lattice. From the central grid point, the velocity vectors point towards all 18 nearest neighbours marked by filled circles. The 19th velocity vector is the rest mode (zero velocity).

The second step: collision¶

The second step is the collision part, where the actual physics happens. For the LBM it is assumed that the collision process linearly relaxes the populations to the local equilibrium, thus that it is a linear (=matrix) operator acting on the populations in each LB cell. It should conserve the particle number and the momentum. At this point it is clear why the mode space is helpful. A 19-dimensional matrix that conserves the first 4 modes (with the eigenvalue 1) is diagonal in the first four rows and columns. By symmetry consideration one finds that only four independent variables are enough to characterize the linear relaxation process so that all symmetries of the lattice are obeyed. Two of them are closely related to the shear and bulk viscosity of the fluid, and two of them do not have a direct physical equivalent. They are just called relaxation rates of the kinetic modes.

In mode space the equilibrium distribution is calculated from the local density and velocity. The kinetic modes 11-19 have the value 0 at equilibrium. The collision operator is diagonal in mode space and has the form

\begin{align*} m^\star_i &= \omega_i \left( m_i - m_i^\text{eq} \right) + m_i ^\text{eq}. \end{align*}

Here $m^\star_i$ is the $i$th mode after the collision. In other words: each mode is relaxed towards its equilibrium value with a relaxation rate $\omega_i$. The conserved modes are not relaxed, i.e. their relaxation rate is 1. We summarize them here:

\begin{align*} m^\star_i &= \omega_i m_i \\ \omega_1=\dots=\omega_4&=1 \\ \omega_5&=\omega_\text{b} \\ \omega_6=\dots=\omega_{10}&=\omega_\text{s} \\ \omega_{11}=\dots=\omega_{16}&=\omega_\text{odd} \\ \omega_{17}=\dots = \omega_{19}&=\omega_\text{even} \\ \end{align*}

To include hydrodynamic fluctuations of the fluid, random fluctuations are added to the nonconserved modes $5\dots 19$ on every LB node so that the LB fluid temperature is well defined and the corresponding fluctuation formula holds, according to the fluctuation dissipation theorem. An extensive discussion of this topic is found in [1]. Thermalization of the fluid is optional in ESPResSo.

Particle coupling¶

In ESPResSo particles are coupled to the LB fluid via the so-called force coupling method: the fluid velocity $\vec{u}$ at the position of a particle is calculated via trilinear interpolation and a force is applied on the particle that is proportional to the velocity difference between particle and fluid:

\begin{align*} \vec{F}_H = - \gamma \left(\vec{v}-\vec{u}\right) \end{align*}

The opposite force is distributed on the surrounding LB nodes. Additionally a random force is added to maintain a constant temperature, according to the fluctuation dissipation theorem.

The coupling scheme between fluid and particles is based on the interpolation of the fluid velocity $\vec{u}$ from the grid nodes. This is done by trilinear interpolation. The difference between the particle velocity $\vec{v}(t)$ and the interpolated velocity $\vec{u}(\vec{r},t)$ is used in the momentum exchange of the equation $\vec{F}_H$ above.

3 The LB interface in ESPResSo¶

ESPResSo features two virtually independent implementations of LB. One implementation uses CPUs and one uses a GPU to perform the computational work. For this, we provide two actor classes LBFluidWalberla and LBFluidWalberlaGPU in the module espressomd.lb.

The LB lattice is a cubic lattice, with a lattice constant agrid in MD units that is the same in all spatial directions. The chosen box length must be an integer multiple of agrid. The LB lattice is shifted by 0.5 agrid in all directions: the node with integer coordinates $\left(0,0,0\right)$ is located at $\left(0.5a,0.5a,0.5a\right)$. The LB scheme and the MD scheme are not synchronized: in one LB time step, several MD steps may be performed. This allows to speed up the simulations and is adjusted with the parameter tau in MD units. The LB parameter tau must be an integer multiple of the MD timestep.

Even if MD features are not used, the system parameters cell_system.skin and time_step must be set. LB steps are performed in regular intervals, such that the timestep $\tau$ for LB is recovered.

Important note: all commands of the LB interface use MD units. This is convenient, as e.g. a particular viscosity can be set and the LB time step can be changed without altering the viscosity. In LB units, both agrid and tau are unity. On the other hand this is a source of a plethora of mistakes: the LBM is only reliable in a certain range of parameters (in LB units) and the unit conversion may take some of them far out of this range. So remember to always make sure you are not messing with that!

One brief example: a certain velocity may be 10 in MD units. If the LB time step is 0.1 in MD units, and the lattice constant is 1.0 in MD units, then it corresponds to a velocity of 1 in LB units. More specifically, given a velocity $v = 10\ \ell^\star\cdot t^{\star-1}$ with $\ell^\star$ the reduced MD length unit and $t^\star$ the reduced MD time unit, and LB parameters $a = 1\ \ell^\star$ and $\tau = 0.1\ t^\star$ in MD units, then the corresponding velocity in LB units is given by $u = v \cdot \tau / a = 10\ \ell^\star\cdot t^{\star-1} \cdot 0.1\ t^\star / 1\ \ell^{\star} = 1$.

In practice, you would like the fluid velocity to be much smaller than the fluid speed of sound $c_s = \frac{1}{\sqrt{3}}\frac{a}{\tau}$ in MD units, aka Mach 1, to avoid numerical instabilities due to the breakdown of the incompressibility assumption. It is usually good practice to avoid exceeding Mach 0.2. At Mach 0.35 the relative error in the calculated fluid density is ~6%, which can ultimately lead to negative populations.

The `LBFluidWalberla` class¶

The LBFluidWalberla class provides an interface to the LB-Method in the ESPResSo core. When initializing an object, one can pass the aforementioned parameters as keyword arguments. Parameters are given in MD units. The available keyword arguments are:

dens: The density of the fluid.
agrid: The lattice constant of the fluid. It is used to determine the number of LB nodes per direction from box_l. They have to be compatible.
visc: The kinematic viscosity
tau: The time step of LB. It has to be an integer multiple of System.time_step.
kT: Thermal energy of the simulated heat bath for thermalized fluids, use 0 to deactivate thermalization.
seed: The random number generator seed, only relevant for thermalized fluids (i.e. kT > 0).
ext_force_density: An external force density applied to every node. This is given as a list, tuple or array with three components.

Using these arguments, one can initialize an LBFluidWalberla object. This object then needs to be added to the system's actor list. The code below provides a minimal example.

import espressomd
import espressomd.lb

# initialize the System and set the necessary MD parameters for LB.
system = espressomd.System(box_l=[31, 41, 59])
system.time_step = 0.01
system.cell_system.skin = 0.4

# Initialize an LBFluidWalberla with the minimum set of valid parameters.
lbf = espressomd.lb.LBFluidWalberla(agrid=1, density=10, kinematic_viscosity=.1, tau=0.01)
# Activate the LB by adding it to the System's actor list.
system.lb = lbf

Sampling data from a node¶

The LBFluidWalberla class also provides a set of methods which can be used to sample data from the fluid nodes. For example lbf[X ,Y ,Z].quantity returns the quantity of the node with $(X, Y, Z)$ coordinates. Note that the indexing in every direction starts with 0. The possible properties are:

velocity: the fluid velocity (list of three floats)
pressure_tensor: the pressure tensor (3x3 matrix)
population: the 19 populations of the D3Q19 lattice.
is_boundary: the boundary flag.
density: the local density.

Slicing is supported, e.g. to obtain all velocity vectors in the LB fluid as a Numpy array, use lbf[:,:,:].velocity.

Setting up boundaries¶

Boundary conditions for the fluid are set on the LBFluidWalberla lattice by marking the nodes at which the boundary condition should hold as boundary nodes. There are several ways to access individual nodes, please refer to the documentation for a complete list. Once they are gathered, a boundary condition e.g. of the type VelocityBounceBack can be assigned to them, as shown in the following example:

node = lbf[0,0,0]
node.boundary = VelocityBounceBack(velocity=[0,0,0])

In order to mark several nodes as boundaries at once, there are a some convenience functions that make it possible, for example, to mark all nodes within a espressomd.shapes as a boundary.

Note that nodes are not marked as boundaries through the periodic boundary if the shape exceeds the edges of the box. If, for example, one would set a sphere with its center in one of the corner of the boxes, only nodes within the sphere fragment will be boundary nodes. To avoid this, make sure the sphere, or any other shape, fits inside the central box.

Here is an example of how to use shapes to mark nodes as boundaries:

import espressomd.shapes

wall_shape = espressomd.shapes.Wall(normal=[1, 0, 0], dist=1)
lbf.add_boundary_from_shape(wall_shape, velocity=[0, 0, 0.01])

This will create a wall shape with a surface normal of $(1, 0, 0)$ at a distance of 1 from the origin of the coordinate system in direction of the normal vector and mark all LB nodes within as boundaries. Additionally, a boundary condition with a velocity of $(0, 0, 0.01)$ is set using the optional velocity argument. For a no-slip boundary condition, leave out the velocity argument, as this will set it to zero by default.

In ESPResSo the so-called link bounce back method is implemented, where the effective hydrodynamic boundary is located midway between boundary and fluid node.